My research focuses on creating theoretical and algorithmic tools to quantify shape in data, blending ideas from various modern approaches to topology and geometry, namely:

• Topological data analysis (TDA), which uses algebraic topology to summarize and quantify local and global shape features in data
• Numerical algebraic geometry, which uses numerical solving methods to compute information about shapes modeled by polynomial equations
• Machine learning, which uses Euclidean geometry and statistics to learn and quantify patterns in data

Efficient Topological Methods for Data Science

Many of the most successful data analysis methods of the past 200 years have been geometric, relying on notions of distances and angles to summarize data. In the last 20, especially, mathematical foundations and algorithms for extracting topological summaries from data have come into focus. Algebraic topology forms the core of these methods, but they interact with category theory, combinatorics, linear algebra, and computational geometry.

I develop theory and algorithms for TDA, with a priority on efficient methods that combine TDA with machine learning for applications.

Recent projects:

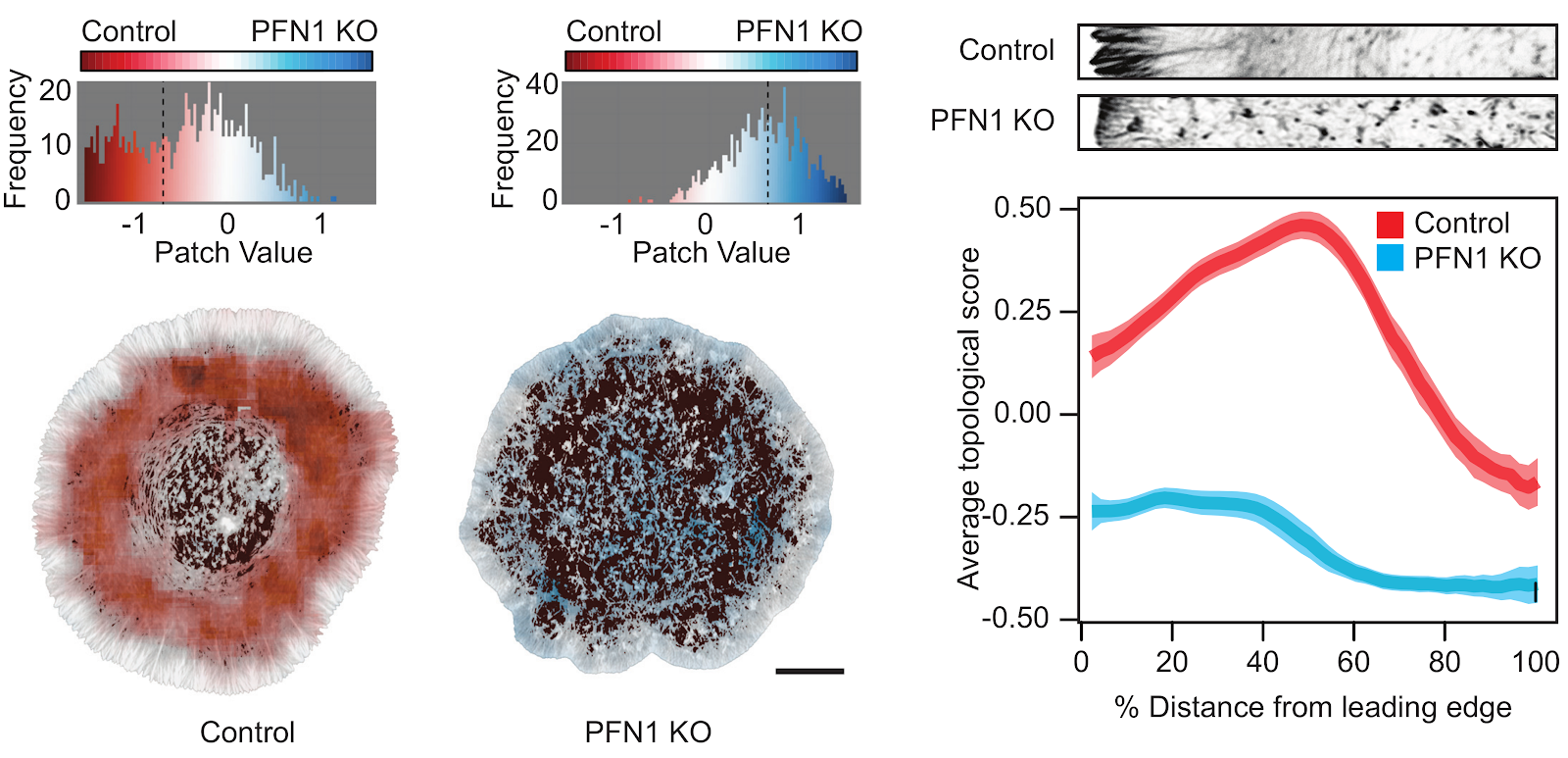
• Topological machine learning to quantify, explore, and generate new hypotheses from topology in microscopy images. Paper.
• Combinatorial foundations for persistence landscapes, one of the main ways to connect persistent homology with machine learning. Paper.
• Topology-inspired methods to aggregate public testimony into communities of interest for use in redistricting. Paper

Topological methods for polynomial data spaces

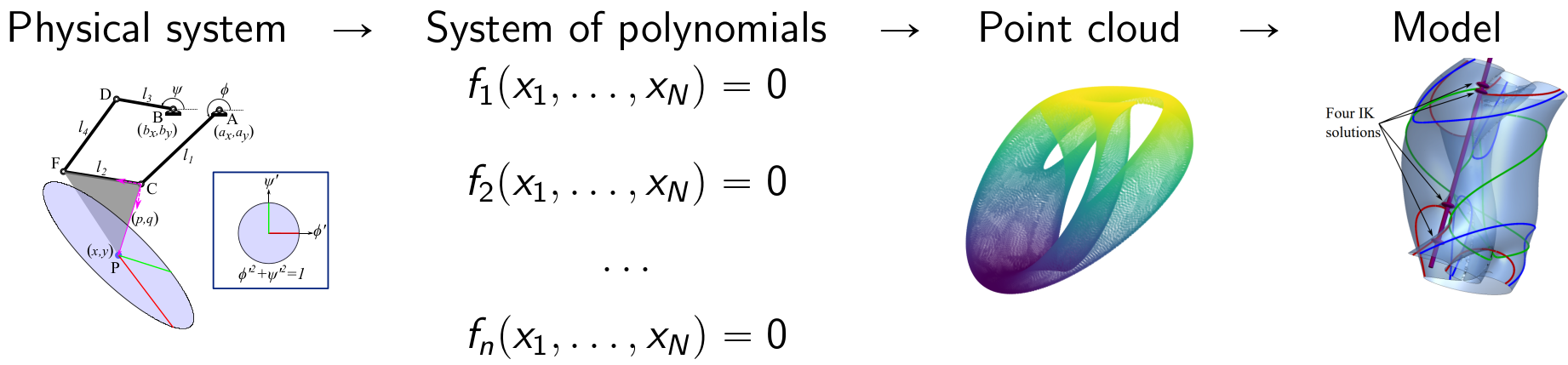
Moving a clock face to different times is easy: push the hands straight to a new position. More complex mechanisms are more challenging, however, because one must coordinate many joints, legs, and motors with more complicated geometric constraints. This part of my research program blends TDA with algebraic, computational, and differential geometry to compute answers to topological questions about shapes modeled by polynomials.

Recent projects:

• Algebraic geometry and algorithms for computing feature sizes of algebraic manifolds. Paper
• Path planning for 5-bar linkages using pipeline. Paper. Video.
• Computing dense point samples on real algebraicspaces from polynomial inputs. Paper